Precalculus Fundamentals, Part I 🧮
⚠️ Under Construction
- When this warning has been removed, the article will be finished.
Content Covered
I thought it would be interesting to create a series of math tutorials spanning from college algebra to calculus. Basic math knowledge is assumed, but I may add descriptions and clarifications for the younger audiences for which the first half of these articles are written. Hopefully my notes will be useful to others going through these courses.
Algebra is a branch of mathematics in which arithmetical operations and formal manipulations are applied to abstract symbols rather than specific numbers. — Britannica (paraphrase)
Here is an outline of my notes, which I used to pass my three month class, with perfect scores, in sixteen days. My notes can be a bit messy, so sorry in advanced:
| Outline | |
|---|---|
| Essential Concepts | Real Numbers, Negative Numbers, Fractions, Absolute Values, Order of Operations |
| Exponents | Properties, Scientific Notation |
| Radicals | Properties, Rational Exponents, Adding & Subtracting, Multiplying, Rationalizing Denominators |
| Polynomials | Defining, Adding & Subtracting, Multiplying & Dividing, Factoring |
| Rational Expressions | Simplifying, Adding & Subtracting, Multiplying & Dividing, Compound |
| Complex Numbers | Properties |
| Logarithms | Properties |
| Equations & Inequalities | Linear, Quadratic, Absolute Value Inequalities, Systems of Equations & Inequalities, Exponential, Logarithmic Equations |
| Functions | Evaluating, Adding & Subtracting, Multiplying & Dividing, Nested, Inverse |
| Applied | Area, Volume, Pythagorean Theorem, Unit Conversion, Arithmetic Sequences, Distance, Rate, Time, Percentage Problems, Mixture Problems, Weighted Average, System of Equations, Geometric Sequences |
The Reunion of Broken Parts
The Strassburg tablet is the oldest recorded use of algebra, dating back to 1800 B.C. during the time of the Old Babylonian Empire. The tablet shows the solution of a quadratic elliptic equation. The Plimpton 322 tablet gives a table of Pythagorean triples in Babylonian Cuneiform script. al-Khwarizmi established algebra as a mathematical discipline that is independent of geometry and arithmetic in his mathematical treatise “The Compendious Book on Calculation by Completion and Balancing,” and it is from his early 9th century book cIlm al-jabr wa l-muqābala “The Science of Restoring and Balancing,” where we get the word for Algebra.
The roots of algebra can be traced to the ancient Babylonians, who developed an advanced arithmetical system with which they were able to do calculations in an algorithmic fashion. The Babylonians developed formulas to calculate solutions for problems typically solved today by using linear equations, quadratic equations, and indeterminate linear equations. By contrast, most Egyptians of this era, as well as Greek and Chinese mathematics in the 1st millennium BC, usually solved such equations by geometric methods, such as those described in the Rhind Mathematical Papyrus, Euclid’s Elements, and The Nine Chapters on the Mathematical Art. — Wikipedia
Essential Concepts
Set Theory, Roster Method, & Set-Builder Notation
A set is a collection of objects whose contents can be clearly determined. The objects in a set are called the elements of the set.
- The Roster method uses commas to separate the elements of the set.
- A set can also be written in Set-builder notation In which the elements of the set are described but not listed.
- Finite sets have a countable number of elements. For example, \(\{a,b,c\}\) is a set of three elements, thus it is a finite set.
- Infinite sets contain an uncountable number of elements. For example, \(\{a,b,c,\dotsc\}\) is a set with an infinite number of elements, thus it is an infinite set.
| Notation | Description |
|---|---|
| \(\{\}\) | Braces indicate the beginning and end of a set notation; elements are separated by commas. |
| \(\dots\) | An ellipsis indicates the continuation of a pattern or an infinite set with no last element i.e. \(\{2, 4, 6, \dotsc, 16, \dotsc\}\) |
| \(\vert\) | This symbol is read “such that”. |
| \(\in\) | “is a member of” or “is an element of” |
| \(\notin\) | “is not a member of” or “is not an element of” |
| \(\varnothing\) | An empty or null set is a set which contains no elements, but which is a subset of all sets. This can also be written as \(\{\}\) |
| Roster Method | \(\{1, 2, 3, 4, 5, 6, 7\}\) |
| Set-Builder | \(\{x \vert x < 8, x \; is \; a \; natural \; number\}\) \(\{x \vert x \leq 7, x \; is \; a \; natural \; number\}\) \(\{x \vert 0 < x < 8, x \; is \; a \; whole \; number\}\) \(\{x \vert 0 < x \leq 7, x \; is \; a \; whole \; number\}\) |
We can also perform operations on sets.
| Notation | Description |
|---|---|
| \(\cap\) | The Intersection of \(A \cap B\) is the set of elements common to both sets. |
| \(\cup\) | The Union of \(A \cup B\) is the set of elements that are members of set A or set B or both. |
The Set of Real Numbers
The five categories of real numbers are natural, whole, integers, rational, and irrational.
The sets that make up the real numbers are referred to as subsets of the real numbers, meaning that all elements in each subset are also elements in the set of real numbers.
- Rational numbers can be written as a ratio of two integers, and their decimal form has a terminating or repeating decimal pattern.
- Irrational numbers cannot be written as a ratio of two integers, and their decimal form has a non-terminating and non-repeating decimal pattern. Rational and irrational numbers together form the set of all real numbers.
| Set of All Real Numbers | \(\mathbb{R} = \{x \vert x \; is \; rational \; or \; x \; is \; irrational\}\) \(\mathbb{R} = \{x \vert x \; is \; rational\} \cup \{x \vert x \; is \; irrational\}\) |
|---|---|
| Set of Rational Numbers | \(\mathbb{Q} = \{x\vert x = \frac{p}{q} \, with \, p \in \mathbb{Z}, q \in \mathbb{Z}, and \, q \ne 0\}\) \(\mathbb{Q} = \{\frac{a}{b} \vert \, a \; and \; b \; are \; integers \; and \; b \ne 0\}\) |
| Set of Irrational Numbers | \(\mathbb{I} = \{x\vert x \in \mathbb{R}, x \notin \mathbb{Q}\}\) |
| \(\sqrt{3}, \sqrt{5}, \sqrt[2]{2}, \sqrt[3]{2}, \sqrt[3]{10}, \frac{3}{\pi^2}, ...\) \(\pi \approx 3.141592..., \, e \approx 2.718281...\) |
| Set of Rational Numbers | \(\mathbb{Q} = \{x\vert x = \frac{p}{q} \, with \, p \in \mathbb{Z}, q \in \mathbb{Z}, and \, q \ne 0\}\) |
|---|---|
| Set of Integers | \(\mathbb{Z} = \{...,-2,-1,0,1,2,...\}\) |
| Set of Whole Numbers | \(\mathbb{N}_{0} \, or \, \mathbb{W} = \{0,1,2,3,...\}\) |
| Set of Natural Numbers (non-negative integers) | \(\mathbb{N} = \{1,2,3,...\}\) |
The Properties of Real Numbers
Subtraction and division neither work with commutative operations nor associative. The number 0 is special for addition; it is called the additive identity because \(a + 0 = a\) for any real number a, in much the same way as the number 1 is special for multiplication; it is called the multiplicative identity because \(a \cdot 1 = a\) for any real number a.
| Commutative Property | Order |
| Commutative Property of Addition | \(a + b = b + a\) |
| Commutative Property of Multiplication | \(ab = ba\) |
| Associative Property | Grouping |
| Associative Property of Addition | \((a + b) + c = a + (b + c)\) |
| Associative Property of Multiplication | \((ab)c = a(bc)\) |
| Distributive Property | |
| Distributive Property of Multiplication over Addition | \(a \cdot (b + c) = a \cdot b + a \cdot c\) \(a(b+c) = ab + ac\) \((b+c)a = ab + ac\) |
| Identity Property | |
| Identity Property of Addition | \(a + 0 = a\) \(0 + a = a\) |
| Identity Property of Multiplication | \(a \cdot 1 = a\) \(1 \cdot a = a\) |
| Inverse Property | |
| Inverse Property of Addition | \(a + (-a) = 0\) \((-a) + a = 0\) |
| Inverse Property of Multiplication | \(a \cdot \frac{1}{a} = 1, \; a \ne 0\) \(\frac{1}{a} \cdot a = 1, \; a \ne 0\) |
The Properties of Negative Numbers
When adding two numbers with matching signs, add the two numbers (as if they are positive) and keep the sign. When adding two numbers with opposite signs, subtract the smaller number from the larger number (as if they are positive), and keep the sign of the larger number. The product or quotient of two positive numbers is positive. The product or quotient of two negative numbers is also positive. The product or quotient of a positive and negative number is negative.
| Properties of Negatives |
|---|
| \((-1)a = -a\) |
| \(-(-a) = a\) |
| \((-a)b = a(-b) = -(ab)\) |
| \((-a)(-b) = ab\) |
| \(-(a+b) = -a-b\) i.e. \(–(a + b) = –1(a + b) = (–1)a + (–1)b = –a + (–b) = –a − b\) |
| \(-(a-b) = b-a\) |
The Properties of Fractions
To add fractions, you must have a common denominator. Fractions that have common denominators are called like fractions. Fractions that have different denominators are called unlike fractions.
| Properties of Fractions | |
|---|---|
| Multiply | \(\frac{a}{b} \cdot \frac{c}{d}=\frac{ac}{bd}\) |
| Divide “Keep, change, flip” |
\(\frac{a}{b} \div \frac{c}{d}=\frac{a}{b} \cdot \frac{d}{c}=\frac{ad}{bc}\) |
| Add (Like Fractions) |
\(\frac{a}{c} + \frac{b}{c}=\frac{a+b}{c}\) |
| Add (Unlike Fractions) |
\(\frac{a}{b} + \frac{c}{d}=\frac{ad+bc}{bd}\) |
| Cancel | \(\frac{ac}{bc} = \frac{a}{b}\) |
| Cross-multiply | \(If \; \frac{a}{b}=\frac{c}{d}, \, then \, ad=bc\) |
We usually find the Least Common Denominator (LCD) when adding unlike fractions. Then we treat them the same way as when we add like fractions. Remember that factors of a number are whole numbers that when multiplied together yield the number. Here is a small refresher on finding the GCF & LCM.
| Find the LCD (The Right Way) | \(\frac{7}{36}+\frac{8}{48}\) |
|---|---|
| Simplify | \(\frac{8}{48}\) |
| Prime factorization of 8 | \(2^3\) |
| Prime factorization of 48 | \(2^4 \cdot 3\) |
| Greatest Common Factor | \(2^3 = 8\) |
| Use Common Factor | \(\frac{8 \, \div \, 8}{48 \, \div \, 8} = \frac{1}{6}\) |
| *Rewrite for clarity | \(\frac{7}{36}+\frac{1}{6}\) |
| Prime factorization of 36 | \(2^2 \cdot 3^2\) |
| Prime factorization of 6 | \(2 \cdot 3\) |
| Use Least Common Multiple | \(2^2 \cdot 3^2 = 36\) |
| \(\frac{a}{c} + \frac{b}{c}=\frac{a+b}{c}\) | \(\frac{7 \, \cdot \, 1}{36 \, \cdot \, 1} + \frac{1 \, \cdot \, 6}{6 \, \cdot \, 6}\) \(\frac{7}{36} + \frac{6}{36} = \frac{7+6}{36} = \frac{13}{36}\) |
If we don’t simplify first, like we did above, we will create more work for ourselves in the longrun.
| Find the LCD (The Long Way) | \(\frac{7}{36}+\frac{8}{48}\) |
|---|---|
| Prime factorization of 36 | \(2^2 \cdot 3^2\) |
| Prime factorization of 48 | \(2^4 \cdot 3\) |
| Use Least Common Multiple | \(2^4 \cdot 3^2 = 144\) |
| \(36 \cdot x = 144\) \(x = \frac{144}{36}\) \(x = 4\) |
|
| \(48 \cdot x = 144\) \(x = \frac{144}{48}\) \(x = 3\) |
|
| \(\frac{a}{c} + \frac{b}{c}=\frac{a+b}{c}\) | \(\frac{7 \, \cdot \, 4}{36 \, \cdot \, 4} + \frac{8 \, \cdot \, 3}{48 \, \cdot \, 3}\) \(\frac{28}{144} + \frac{24}{144} = \frac{28 + 24}{144} = \frac{52}{144}\) |
| Simplify | \(\frac{52}{144}\) |
| Prime factorization of 52 | \(2^2 \cdot 13\) |
| Prime factorization of 144 | \(2^4 \cdot 3^2\) |
| Greatest Common Factor | \(2^2 = 4\) |
| Use Common Factor | \(\frac{52 \, \div \, 4}{144 \, \div \, 4} = \frac{13}{36}\) |
This method is better for computer algorithms rather than a method used by hand, although the euclidean algorithm is just about as handy as a factor tree when finding the GCF.
| Solving without LCD (Textbook) | \(\frac{7}{36}+\frac{8}{48}\) |
|---|---|
| Cross-multiply then divide over the product of the denominators \(\frac{a}{b} + \frac{c}{d}=\frac{ad+bc}{bd}\) |
\(\frac{7 \, \cdot \, 48 \, + \, 36 \, \cdot \, 8}{36 \, \cdot \, 48}\) |
| Simplify | \(\frac{624}{1728}\) |
| Find GCF via Euclidean Algorithm | 48 |
| Use the GCF to find the result | \(\frac{624 \, \div \, 48}{1728 \, \div \, 48} = \frac{13}{36}\) |
Absolute Values
The important thing to remember, in context to addition and subtraction, is to evaluate the absolute value first, and then perform the mathematical operations. The absolute value sign acts as a grouping symbol, not unlike a parenthetical. When multiplying and dividing absolute values, the product and quotient properties of absolute values will allow us to simplify absolute value expressions.
| Definition of Absolute Value | \(\lvert a\rvert = \begin{cases}\quad a, & if \, a \ge 0\\ \, -a, & if \, a \lt 0\\ \end{cases}\) |
|---|---|
| The absolute value of a number is always positive or zero. | \(\lvert a\rvert \ge 0\) |
| A number and its negative have the same absolute value. | \(\lvert a\rvert = \lvert -a\rvert\) |
| The absolute value of a product is the product of the absolute values. | \(\lvert ab\rvert = \lvert a\rvert \lvert b\rvert\) |
| The absolute value of a quotient is the quotient of the absolute values. | \(\lvert \frac{a}{b}\rvert = \frac{\lvert a\rvert}{\lvert b\rvert}\) |
| Triangle Inequality | \(\lvert a+b\rvert \le \lvert a\rvert + \lvert b\rvert\) |
📏 The Order of Operations
When PEMDAS becomes unclear, remember that math problems are solved left to right. Multiplication has the same precedence as division. The same is true of addition and subtraction. Grouping symbols fall under parentheses in PEMDAS, they include fraction bars, absolute value signs, and radicals.
| PE(MD)(AS) | \(8 \div 2(2+2)\) |
|---|---|
| (P)arentheses | \(8 \div 2 \cdot 4\) |
| (E)xponents or Square Roots |
N/A |
| (M)ultiplication or (D)ivision Left-to-Right! |
\(4 \cdot 4\) 16 |
| (A)ddition or (S)ubtraction Left-to-Right! |
N/A |
| PE(MD)(AS) | \(10 \cdot 4 - 2 \cdot (4^2 \div 4) \div 2 \div \frac{1}{2} + 10\) |
|---|---|
| (P)arentheses | \((4^2 \div 4)\) You could cancel \(4^2 \div 4 = \frac{4^2}{4} = \frac{4 \, \cdot \cancel{4}}{\cancel{4}} = \frac{4}{1} = 4\) See (E)xponents |
| (E)xponents | \((4^2 \div 4) = (16 \div 4) = 4\) \(10 \cdot 4 - 2 \cdot 4 \div 2 \div \frac{1}{2} + 10\) |
| (M)ultiplication (D)ivision |
\(40 - 2 \cdot 4 \div 2 \div \frac{1}{2} + 10\) \(40 - 8 \div 2 \div \frac{1}{2} + 10\) \(40 - 4 \div \frac{1}{2} + 10\) \(40 - 4 \cdot 2 + 10\) \(40 - 8 + 10\) |
| (A)ddition (S)ubtraction |
\(32 + 10\) 42 |
📏 Exponents
The word exponent comes from the Latin “expo” meaning “out of” and “ponere” meaning “place.” The Babylonians living in present day Iraq were the first to work with exponents, dating back to the 23rd century BC or earlier!
| Laws of Exponents | |
|---|---|
| Product Property \(a^ma^n=a^{m+n}\) |
\(a^3a^2 = (aaa)(aa) = a^5\) |
| Quotient Property \(\frac{a^m}{a^n}=a^{m-n}\) |
\(\frac{a^5}{a^2} = \frac{aaaaa}{aa} = aaa = a^3\) |
| Power of Power \((a^m)^n=a^{m \cdot n}\) |
\((a^2)^3 = a^2\cdot a^2\cdot a^2 = a^6\) |
| Power of Product \((ab)^n=a^nb^n\) |
\((ab)^3 = (ab)(ab)(ab) = a^3b^3\) |
| Power of Quotient \((\frac{a}{b})^n=\frac{a^n}{b^n}\) |
\((\frac{a}{b})^3 = (\frac{a}{b})(\frac{a}{b})(\frac{a}{b}) = \frac{a^3}{b^3}\) |
| Additional Properties of Exponents | |
| Definition of Rational or Property of Fractional Exp. \(a^{\frac{m}{n}} = (\sqrt[n]{a})^m\) \(a^{\frac{m}{n}} = \sqrt[n]{a^m}\) |
\((\sqrt[6]{3x})^5 = (3x)^{\frac{5}{6}}\) |
| \(\frac{1}{(\sqrt[3]{xy})^2} = (xy)^{-\frac{2}{3}}\) | |
| Zero Property \(a^0=1, \, if \, a \ne 0\) |
\(7^0 = 1\) \((7x^3)^0 = 1\) \((-8)^0 = 1\) \(-8^0 = -1\) |
| Property of Negative Ex. \(a^{-n}=\frac{1}{a^n}, \, if \, n \gt 0\) |
\(\frac{a^3b^{-2}c}{2d^{-1}e^{-4}f^2} = \frac{a^3cde^4}{2b^2f^2}\) |
| Property of Negative Ex. \((\frac{b}{a})^{-n} =\frac{b^{-n}}{a^{-n}}=\frac{a^{n}}{b^{n}}=(\frac{a}{b})^n\) |
\(7^{-3} = \frac{1}{7^3} = \frac{1}{343}\) |
| Property of Negative Ex. \(\frac{b^{-m}}{a^{-n}} = \frac{a^n}{b^m}\) |
📏 Scientific Notation
The Greek mathematician Archimedes (287 BC - 212 BC), developed a system for representing large numbers using a system very similar to scientific notation. Scientific notation is a way to express numbers as the product of a decimal number and a power of 10. It is important to remember that when you’re writing numbers in scientific notation, you can only have one non-zero digit to the left of the decimal, but you can have any number of digits to the right. When you’re writing in scientific notation, Keep in mind:
- Moving the decimal to the left is going to increase your exponent
- Moving the decimal to the right is going to decrease your exponent
- A positive exponent indicates moving the decimal to the right
- A negative exponent indicates moving the decimal to the left
Let’s make use of the article Orders of Magnitude, and for the sake of simplicity we will define:
Solar Massas \(M_☉ \approx 2 \times 10^{30}\)Earth Massas \(M_🜨 \approx 6 \times 10^{24}\)
| Scientific Notation | Mass In Kilograms |
|---|---|
| General Sherman (The trunk of the largest living tree) \(1 \times 10^6 \, kg\) |
One Million Kilograms 1,000,000 kg |
| Great Pyramid of Giza \(6 \times 10^9 \, kg\) |
Six Billion Kilograms 6,000,000,000 kg |
| Total mass of the world’s human population \(4 \times 10^{11} \, kg\) |
Four-Hundred Billion Kilograms 400,000,000,000 kg |
| A teaspoon (5 ml) of neutron star material \(5.5 \times 10^{12} \, kg\) |
Five Trillion Five Hundred Billion Kilograms 5,500,000,000,000 kg 12,125,424,420,168 lbs 6,062,712,210.0841 US Tons |
| Mount Everest \(2.96471\times 10^{14} \, kg\) |
Two-Hundred and Ninety Six Trillion Four-Hundred and Seventy One Billion Kilograms 296,471,000,000,000 kg |
| Earth’s Atmosphere \(5.1\times 10^{18} \, kg\) |
Five Quintillion One-Hundred Quadrillion Kilograms 5,100,000,000,000,000,000 kg |
| Earth’s Oceans \(1.4\times 10^{21} \, kg\) |
One-Sextillion Four-Hundred Quintillion Kilograms 1,400,000,000,000,000,000,000 kg |
| The Moon (Earth’s Moon) \(7.3\times 10^{22} \, kg\) |
Seventy-Three Sextillion Kilograms 73,000,000,000,000,000,000,000 kg |
| The Planet Earth \(6\times 10^{24} \, kg\) |
Six Septillion Kilograms 6,000,000,000,000,000,000,000,000 kg 1 \(M_🜨\) Earth Mass |
| The Sun \(2 \times 10^{30} \, kg\) |
Two Nonillion Kilograms 2,000,000,000,000,000,000,000,000,000,000 kg One Solar Mass \(1 M_☉\) \(\approx\) Three-Hundred and Thirty Three Thousand Earth Masses \(333,333.\bar{33} \, M_🜨\) |
| Sagittarius A* Supermassive black hole at the center of the Milky Way \(7–8\times 10^{36} \, kg\) |
Eight Undecillion Kilograms 8,000,000,000,000,000,000,000,000,000,000,000,000 kg Four Million Solar Masses 4,000,000 \(M_☉\) |
| Ton 618 Ultramassive black hole \(6.6 \times 10^{10} * 1 \, M_☉\) \(\approx 1.32 \times 10^{41}\) |
One Hundred and Thirty Two Duodecillion 132,000,000,000,000,000,000,000,000,000,000,000,000,000 kg Sixty-Six Billion Solar Masses 66,000,000,000 \(M_☉\) |
| The Milky Way Galaxy \(1.2\times 10^{42} \, kg\) |
One Tredecillion Two-Hundred Duodecillion Kilograms 1,200,000,000,000,000,000,000,000,000,000,000,000,000,000 kg Six-Hundred Billion Solar Masses 600,000,000,000 \(M_☉\) |
| Local Group \(2–3\times 10^{42} \, kg\) |
3,000,000,000,000,000,000,000,000,000,000,000,000,000,000 kg One-Trillon Five Hudred Billion Solar Masses 1,500,000,000,000 \(M_☉\) |
| Hercules–Corona Borealis Great Wall (The largest structure in the known universe) \(4\times 10^{49} \, kg\) |
40 Quindecillion Kilograms 40,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 kg Twenty Quintillion Solar Masses 20,000,000,000,000,000,000 \(M_☉\) |
| Mass of the observable universe \(4.4506\times 10^{52} \, kg\) to \(6\times 10^{52} \, kg\) |
Sixty Sexdecillion Kilograms 60,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 kg Thirty Sextillion Solar Masses 30,000,000,000,000,000,000,000 \(M_☉\) |
Multiplication & Division With Scientific Notation
When multiplying and dividing in scientific notation, deal with the non-exponential and exponential (containing the power of 10) separately. Multiply or divide the decimal number part first, then multiply or divide the part with exponents, applying the property of exponents to either add or subtract the exponents
| Multiplication | \((2.1\times 10^{-7})(3.7\times 10^5)\) |
|---|---|
| Deal with Numbers First | \(2.1\cdot 3.7 = 7.77\) |
| Use Product Property on Exponents | \(10^{-7}\cdot 10^5\) |
| \(10^{-7+5} = 10^{-2}\) | |
| Solution | \(7.77\times 10^{-2}\) |
Often when we multiply or divide in scientific notation the end result is not in scientific notation. We will then have to convert the front number into scientific notation and then combine the 10’s using the product property of exponents and adding the exponents.
| Earth Times The Sun | \((6\times 10^{24})(2\times 10^{30})\) |
|---|---|
| Deal with Numbers First | \(6\cdot 2 = 12\) |
| Convert to Scientific Notation | \(1.2\times 10^1\) |
| Use Product Property on Exponents | \(10^1\cdot 10^{24}\cdot 10^{30}\) |
| \(10^{1+24+30} = 10^{55}\) | |
| Solution | \(1.2\times 10^{55}\) |
| Earth Cubed | \((6\times 10^{24})^3\) |
|---|---|
| Power of Product Rule | \((6)^3\times (10^{24})^3\) |
| Deal with Numbers First | \(6^3 = 216\) |
| Convert to Scientific Notation | \(2.16\times 10^2\) |
| *Rewrite for Clarity | \(2.16\times 10^2\cdot (10^{24})^3\) |
| Use Power of Power Rule on Exponents | \((10^{24})^3 = 10^{24\cdot 3} = 10^{72}\) |
| *Rewrite for Clarity | \(2.16\times 10^2\cdot 10^{72}\) |
| Use Product Property on Exponents | \(10^2\cdot 10^{72} = 10^{2+72} = 10^{74}\) |
| Solution | \(2.16\times 10^{74}\) |
A similar process is used to divide in scientific notation. First, we divide the decimal part of the number, and then apply a property of exponents to easily divide the powers of 10.
| Division | \(\frac{4.96\times 10^4}{3.1\times 10^{-3}}\) |
|---|---|
| Deal with Numbers First | \(\frac{4.96}{3.1} = 1.6\) |
| Use Quotient Property on Exponents | \(\frac{10^4}{10^{-3}}\) |
| \(10^{4-(-3)} = 10^{4+3} = 10^7\) | |
| Solution | \(1.6\times 10^7\) |
| The Sun Divided By The Earth | \(\frac{2\times 10^{30}}{6\times 10^{24}}\) |
|---|---|
| Deal with Numbers First | \(\frac{2}{6} = 0.3333333333333333\) |
| Convert to Scientific Notation | \(3.333333333333333\times 10^{-1}\) |
| Use Quotient Property on Exponents | \(\frac{10^{30}}{10^{24}}\) |
| \(10^{30-24} = 10^6\) | |
| Use Product Property on Exponents | \(10^{-1}\cdot 10^6\) |
| \(10^{-1+6} = 10^5\) | |
| Solution | \(3.333333333333333\times 10^5 \, kg\) |
| 1 \(M_☉\) 333,333.333333333333333 \(M_🜨\) |
| Earth Times The Sun Divided By The Moon |
\((6\times 10^{24})(2\times 10^{30}) \over 7.3\times 10^{22}\) |
|---|---|
| Solution from above | \(1.2\times 10^{55} \over 7.3\times 10^{22}\) |
| Deal with Numbers First | \(\frac{1.2}{7.3} = 0.1643835616438356\) |
| Convert to Scientific Notation | \(0.1643835616438356 = 1.643835616438356\times 10^{-1}\) |
| *Rewrite for Clarity | \(1.643835616438356\times 10^{-1} \cdot \frac{10^{55}}{10^{22}}\) |
| Use Quotient Property | \(\frac{10^{55}}{10^{22}}=10^{55-22}=10^{33}\) |
| *Rewrite for Clarity | \(1.643835616438356\times 10^{-1} \cdot 10^{33}\) |
| Use Product Property | \(10^{-1}\cdot 10^{33} = 10^{-1+33} = 10^{32}\) |
| Solution | \(1.643835616438356\times 10^{32}\) |
Addition & Subtraction With Scientific Notation
| Addition (Like Powers) A teaspoon (5 ml) of neutron star material (5000 million tonnes) |
\((5.5\times 10^{12})+(5.5\times 10^{12})\) |
|---|---|
| Group Decimals First | \((5.5+5.5)\times 10^{12}\) |
| Convert to Scientific Notation | \(11\times 10^{12} = 1.1\times 10^{13}\) |
| Solution (2 teaspoons) |
\(1.1\times 10^{13}\) |
| Subtraction (Like Powers) The Milky Way Galaxy from the Local Group |
\((3\times 10^{42})-(1.2\times 10^{42})\) |
|---|---|
| Group Decimals First | \((3-1.2)\times 10^{42} = 1.8\times 10^{42}\) |
| Solution | \(1.8\times 10^{42}\) |
| Subtraction (Like Powers) The Milky Way Galaxy from the Local Group |
\((2\times 10^{42})-(1.2\times 10^{42})\) |
|---|---|
| Group Decimals First | \((2-1.2)\times 10^{42} = 0.8\times 10^{42}\) |
| Convert to Scientific Notation | \(0.8\times 10^{42} = 8\times 10^{41}\) |
| Solution | \(8\times 10^{41}\) |
Remember that when converting into scientific notation, if we move the decimal to the left, this increases the exponent. If we move the decimal to the right, this decreases the exponent. Note that it does not matter which number you choose to rewrite. We would get the same result if we chose to rewrite the other number.
| Addition (Unlike Powers) Earth’s Atmosphere and Oceans |
\((5.1\times 10^{18}) + (1.4\times 10^{21})\) |
|---|---|
| Rewrite to have a common power | \((5.1\times 10^{18}) + (1400\times 10^{18})\) |
| Group Numbers First | \((5.1+1400)\times 10^{18} = 1405.1\times 10^{18}\) |
| Convert to Scientific Notation | \(1.4051\times 10^{21}\) |
| Subtraction (Unlike Powers) Earth’s Atmosphere and Oceans from Earth’s Mass |
\((6\times 10^{24})-(1.4051\times 10^{21})\) |
|---|---|
| Rewrite to have a common power | \((6000\times 10^{21})-(1.4051\times 10^{21})\) |
| Group Numbers First | \((6000-1.4051)\times 10^{21} = 5998.5949\times 10^{21}\) |
| Convert to Scientific Notation | \(5.9985949\times 10^{24}\) |
📏 Radicals
Just as multiplication and division are inverse operations of one another, radicals and exponents are also inverse operations of each other, meaning they cancel each other out. Fractional exponents and radicals can be written as one another by using the property of fractional exponents. The largest advantage of being able to change a radical expression into an exponential expression is that we are now allowed to use all of our exponent properties to simplify.
| Properties of Radicals | |
|---|---|
| Definition of nth root \(\sqrt[n]{a}=b, \, means \, b^n=a\) By the definition of nth root \(a^{\frac{1}{n}}=\sqrt[n]{a}\) |
\((a^{\frac{1}{n}})^n=a^{(\frac{1}{n})n}=a^1=a\) |
| Root of a power \(\sqrt[n]{a^m}=(\sqrt[n]{a})^m, \, if \, a \ge 0\) |
|
| Product Property \(\sqrt[n]{ab} = \sqrt[n]{a} \cdot \sqrt[n]{b}\) \(\sqrt[n]{x} \cdot \sqrt[n]{x} = x\) |
\(\sqrt[3]{27xy^3} = \sqrt[3]{27}\cdot \sqrt[3]{x}\cdot \sqrt[3]{y^3}\) \(3\cdot \sqrt[3]{x}\cdot y = 3y\sqrt[3]{x}\) |
| Definition of Rational or Property of Fractional Exp. \(a^{\frac{m}{n}} = (\sqrt[n]{a})^m\) \(a^{\frac{m}{n}} = \sqrt[n]{a^m}\) |
\((\sqrt[6]{3x})^5 = (3x)^{\frac{5}{6}}\) \(\frac{1}{(\sqrt[3]{xy})^2} = (xy)^{-\frac{2}{3}}\) |
| Quotient Property \(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}, \, if \, b \ne 0\) |
\(\frac{\sqrt[3]{x^2y}}{\sqrt[3]{8xy^2}} = \sqrt[3]{\frac{x^2y}{8xy^2}}\) \(\sqrt[3]{\frac{x}{8y}} = \sqrt[3]{\frac{1}{8}\cdot \frac{x}{y}}\) \(\frac{\sqrt[3]{1}}{\sqrt[3]{8}}\cdot \sqrt[3]{\frac{x}{y}} = \frac{1}{2}\sqrt[3]{xy^{-1}}\) |
| \(\sqrt[n]{a^n} = a, \, if \, n \, is \, odd\) \(\sqrt[n]{a^n} = |a|, \, if \, n \, is \, even\) |
|
| Root of a root \(\sqrt[m]{\sqrt[n]{a}}=\sqrt[m \cdot n]{a}\) |
\(\sqrt{\sqrt[3]{729}} = \sqrt[6]{729} = 3\) \(\sqrt{x\sqrt{x}} = \sqrt{xx^{\frac{1}{2}}}\) \(\sqrt{xx^{\frac{1}{2}}} = (xx^{\frac{1}{2}})^{\frac{1}{2}}\) \((x^{\frac{1}{1}}\cdot x^{\frac{1}{2}})^{\frac{1}{2}} = (x^{\frac{1}{1}+\frac{1}{2}})^{\frac{1}{2}}\) \((x^{\frac{3}{2}})^{\frac{1}{2}} = x^{\frac{3}{4}}\) \(\sqrt[4]{x^3} = (\sqrt[4]{x})^3 = (x^3)^{\frac{1}{4}} = x^{\frac{3}{4}}\) |
📏 Rational or Fractional Exponents and Radicals
| Simplify | \(\sqrt[6]{y^5}\sqrt[3]{y^2}\) |
|---|---|
| Rewrite as Rational Exponents | \(y^{\frac{5}{6}} \cdot y^{\frac{2}{3}}\) |
| Product Property of Exponents | \(y^{\frac{5}{6}+\frac{2}{3}}\) |
| Find the LCM of 6 & 3 | \(6 = 2 \cdot 3\) \(3 = 1 \cdot 3\) \(LCM \; is \; 6\) |
| Add Unlike Fractions w\ LCD | \((\frac{5 \, \cdot \, 1}{6 \, \cdot \, 1}) + (\frac{2 \, \cdot \, 2}{3 \, \cdot \, 2}) = \frac{5+4}{6}\) |
| Find the GCF of 9 & 6 | \(9 = 3^2\) \(3 = 1 \cdot 3\) \(GCF \; is \; 3\) |
| Simplify Fraction \w GCD | \(\frac{9 \, \div \, 3}{6 \, \div \, 3} = \frac{3}{2}\) |
| Solution | \(y^{\frac{3}{2}}\) |
| Simplify | \(\sqrt[3]{y\sqrt{y}} = y^{\frac{1}{2}}\) |
|---|---|
| Definition of Rational Exponents | \(\sqrt[3]{y\sqrt[2]{y^1}} = \sqrt[3]{y\cdot y^{\frac{1}{2}}}\) |
| Definition & Product Property | \((y\cdot y^{\frac{1}{2}})^{\frac{1}{3}} = (y^{\frac{1}{1} + \frac{1}{2}})^{\frac{1}{3}} = (y^{\frac{2}{2} + \frac{1}{2}})^{\frac{1}{3}}\) |
| Power of power property | \((y^{\frac{3}{2}})^{\frac{1}{3}} = y^{\frac{3}{2}\cdot \frac{1}{3}} = y^{\frac{3}{6}}\) |
| Solution | \(y^{\frac{1}{2}}\) |
📏 Adding & Subtracting Radical Expressions
Two or more square roots can be combined using the distributive property if they have the same radicand (number underneath the radical sign). Radicals are called like radicals if they have the same radicand and the same index (square root, cubed root, or fifth root). Sometimes you can break down a radicand into factors to simplify the radicand, you might then be able to combine it with another like term. In many ways, like radicals are analogous to like terms.
| Adding Like Radicals | \(7\sqrt{8}+6\sqrt{8}\) |
|---|---|
| Apply Distributive Property | \((7+6)\sqrt{8}\) \(13\sqrt{8}\) |
| Simplify | \(13 \cdot \sqrt{2 \cdot 4}\) \(13 \cdot \sqrt{4} \cdot \sqrt{2}\) \(13 \cdot 2 \cdot \sqrt{2}\) \(26\sqrt{2}\) |
| Subtracting Like Radicals | \(7\sqrt{12}-8\sqrt{12}\) |
|---|---|
| Apply Distributive Property | \((7-8)\sqrt{12}\) \(-1\sqrt{12}\) |
| Simplify | \(-1 \cdot \sqrt{4 \cdot 3}\) \(-1 \cdot \sqrt{4} \cdot \sqrt{3}\) \(-1 \cdot 2 \cdot \sqrt{3}\) \(-2\sqrt{3}\) |
When dealing with radicals with an unlike radicand, the first step is to simplify the radicands first.
| Unlike Radicals | \(4\sqrt{50x} - 6\sqrt{32x}\) |
|---|---|
| Simplify | \(4 \cdot \sqrt{50 \cdot x} - 6 \cdot \sqrt{32 \cdot x}\) \(4 \cdot \sqrt{25 \cdot 2 \cdot x} - 6 \cdot \sqrt{16 \cdot 2 \cdot x}\) \(4 \cdot 5 \cdot \sqrt{2 \cdot x} - 6 \cdot 4 \cdot \sqrt{2 \cdot x}\) \(20 \cdot \sqrt{2x} - 24 \cdot \sqrt{2x}\) |
| Apply Distributive Property | \((20-24) \cdot \sqrt{2x}\) \(-4\sqrt{2x}\) |
📏 Multiplying Radical Expressions
| Multiplying Radicals Using Distribution | \(\sqrt{7}(8+\sqrt{7})\) |
|---|---|
| Distribute the square root of 7 | \(\sqrt{7} \cdot 8 + \sqrt{7} \cdot \sqrt{7}\) |
| Simplify \(\sqrt{7} \cdot \sqrt{7} \; to \; 7\) | \(8 \cdot \sqrt{7} + 7\) |
| Solution | \(7 + 8\sqrt{7}\) |
| Multiplying Radicals Using FOIL | \((\sqrt{3}+6)(12-\sqrt{3})\) |
|---|---|
| FOIL (First) | \(\sqrt{3} \cdot 12\) |
| FOIL (Outside) | \(\sqrt{3} \cdot -\sqrt{3}\) |
| FOIL (Inside) | \(6 \cdot 12\) |
| FOIL (Last) | \(6 \cdot -\sqrt{3}\) |
| Group like terms | \((\sqrt{3} \cdot 12) + (\sqrt{3} \cdot -\sqrt{3}) + (6 \cdot 12) + (6 \cdot -\sqrt{3})\) |
| Combine | \((12\sqrt{3}) + (-3) + (72) + (-6\sqrt{3})\) \((12\sqrt{3}) + (-6\sqrt{3}) + (72) + (-3)\) |
| Solution | \(6\sqrt{3} + 69\) |
Rationalizing The Denominator or Numerator
If a fraction has a denominator of this form, we may rationalize the denominator by multiplying numerator and denominator by the conjugate radical. Radical expressions that involve the sum and difference of the same two terms are called conjugates.
| Rationalizing | \(A+B\sqrt{C}\) |
|---|---|
| Conjugate Radical | \((A-B\sqrt{C})\) |
| Multiply | \((A+B\sqrt{C})(A-B\sqrt{C})\) |
| notes* | \(A^2-B^2C\) |
*This works because, by special product forumla: \((A+B)(A-B)=A^2-B^2\), the product of the denominator and its conjugate radical does not contain a radical.
| Rationalizing | \(\frac{1}{1+\sqrt{2}}\) |
|---|---|
| Conjugate Radical | \(1-\sqrt{2}\) |
| Multiply | \(\frac{1}{1+\sqrt{2}} \cdot \frac{1-\sqrt{2}}{1-\sqrt{2}}\) |
| \(\frac{1 \cdot 1 - \sqrt{2}}{(1+\sqrt{2})(1-\sqrt{2})}\) | |
| \(\frac{1 - \sqrt{2}}{(1)^2-(\sqrt{2})^2}\) | |
| \(\frac{1 - \sqrt{2}}{1-2}\) | |
| Any expression divided by -1 equals it’s opposite. Any expression divided by it’s opposite equals -1. |
\(\frac{1 - \sqrt{2}}{-1}\) |
| \(-(1 - \sqrt{2})\) | |
| \(\sqrt{2}-1\) |
| Rationalizing | \(\frac{\sqrt{4+h}-2}{h}\) |
|---|---|
| \(\frac{\sqrt{4+h}-2}{h} \cdot \frac{\sqrt{4+h}+2}{\sqrt{4+h}+2}\) | |
| \(\frac{(\sqrt{4+h})^2-(2)^2}{h(\sqrt{4+h}+2)}\) | |
| \(\frac{4+h-4}{h(\sqrt{4+h}+2)}\) | |
| \(\frac{h}{h(\sqrt{4+h}+2)}\) | |
| Cancel | \(\frac{1}{\sqrt{4+h}+2}\) |
Polynomials
\[a_nx^n+a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + \dots + a_1x + a_0,\]A polynomial is composed of a single term or a sum of two or more terms containing variables with whole-number exponents. If a polynomial can be considered simplified when it contains no grouping symbols and no like terms, then a simplified polynomial of precisely one term is called a monomial. A simplified polynomial of two and three terms are referred to as a binomial and a trinomial respectively. Simplified polynomials with four or more terms have no special names.
Another way of looking at it might be to say that a polynomial is simply a sum of monomials, a binomial is a sum of two monomials, and a trinomial is the sum of three monomials. The standard form of a polynomial is written with the terms in the order of descending powers of the variable. The degree of a polynomial is the greatest degree of all the terms of the polynomial.
| Defining Polynomials | |
|---|---|
| Linear (\(x^1\)) Binomial (2 Terms) | \(5x+1\) |
| Quadratic (\(x^2\)) Trinomial (3 Terms) | \(2x^2-3x+4\) |
| Cubic (\(x^3\)) Four Term Polynomial (Not written in standard form) |
\(3-x+x^2-\frac{1}{2}x^3\) |
📏 Adding & Subtracting Polynomials
| Adding Polynomials | |
|---|---|
| Find the sum | \((x^3-6x^2+2x+4) + (x^3+5x^2-7x)\) |
| Group Like Terms | \((x^3+x^3) + (-6x^2+5x^2) + (2x-7x) + 4\) |
| Combine Like Terms | \(2x^3 - x^2 - 5x + 4\) |
| Subtracting Polynomials | |
|---|---|
| Find the difference | \((x^3-6x^2+2x+4) - (x^3+5x^2-7x)\) |
| Distribute Negative | \(x^3-6x^2+2x+4-x^3-5x^2+7x\) |
| Group Like Terms | \((x^3-x^3) + (-6x^2-5x^2) + (2x+7x) + 4\) |
| Combine Like Terms | \(-11x^2 + 9x + 4\) |
📏 Multiplying Polynomials
| Multiplying Binomials Using FOIL | \((2x+1)(3x-5)\) |
|---|---|
| (F)irst | \(2x \cdot 3x=\bf6x^2\) |
| (O)uter | \(2x-5=\bf-10x\) |
| (I)nner | \(1 \cdot 3x=\bf3x\) |
| (L)ast | \(1 \cdot -5=\bf-5\) |
| Group like terms | \(\bf6x^2-10x+3x-5\) |
| Combine like terms | \(6x^2-7x-5\) |
| Multiplying Polynomials | \((2x+3)(x^2-5x+4)\) |
|---|---|
| Distribute | \(2x(x^2-5x+4) \, \boldsymbol{+} \, 3(x^2-5x+4)\) |
| \((2x^3-10x^2+8x) + (3x^2-15x+12)\) | |
| Group like terms | \(2x^3 + (-10x^2+3x^2) + (8x-15x) + 12\) |
| Combine like terms | \(2x^3-7x^2-7x+12\) |
Dividing Polynomials
| Dividing by a Monomial | \(18x^3-15x^2+9x+6 \over 3x\) |
|---|---|
| All the terms have a common factor of 3x | \(3x(6x^2)-3x(5x)+3x(3)+3(2) \over 3x\) |
| Divide each term in the numerator by the denominator | \(\frac{3x(6x^2)}{3x}-\frac{3x(5x)}{3x}+\frac{3x(3)}{3x}+\frac{3(2)}{3x}\) |
| Solution | \(6x^2-5x+3+\frac{2}{x}\) |
Factoring Polynomials
| Factoring Binomials | \(3x^2-6x\) |
|---|---|
| Find the GCF | \(3x\) |
| Factored | \(\boldsymbol{3x}(x-2)\) |
| Factoring Trinomials | \(8x^4y^2+6x^3y^3-2xy^4\) |
|---|---|
| Find the GCF | \(2xy^2\) |
| \(8, 6, -2\) have a GCF of \(\bf2\) | |
| \(x^4, x^3, x\) have a GCF of \(\bf{x}\) | |
| \(2xy^2\) is the GCF of the trinomial | |
| Factored | \(2xy^2(4x^3+3x^2y-y^2)\) |
| Factoring Four Terms | \((2x+4)(x-3)-5(x-3)\) |
|---|---|
| Find the GCF | \((x-3)\) |
| Sometimes, the GCF of an expression is not just a monomial but an entire parenthetical quantity. The two terms \((2x+4)\) and \(-5\) have a common factor \((x-3)\) | |
| Factored | \([(2x+4)-5](x-3)\) |
| Distribute & Simplify | \((2x-1)(x-3)\) |
Factoring A Polynomial With Fractional Exponents
| Polynomial with Fractional Exponents | \(3x^{\frac 3 2}-9x^{\frac 1 2}+6x^{-\frac 1 2}\) |
|---|---|
| Factor out \(3x^{-\frac 1 2}\) | \(3x^{-\frac 1 2}(x^2-3x+2)\) |
| To factor out the \(x^{-\frac 1 2}\) from \(x^{\frac 3 2}\), we subtract exponents |
\(x^{-\frac 1 2}(x^{\frac{3}{2}-(-\frac{1}{2})})\) \(x^{-\frac 1 2}(x^{\frac{3}{2}+\frac{1}{2}})\) \(x^{-\frac 1 2}(x^2)\) |
| Factor Quadratic | \(3x^{-\frac 1 2}(x-1)(x-2)\) |
Special Product & Factoring Formulas
If A and B are any real numbers or algebraic expressions, then …
| Difference of Squares |
|---|
| \(A^2-B^2=(A-B)(A+B)\) |
| \(4x^2-25\) \((2x)^2-5^2\) \((2x-5)(2x+5)\) |
| \((x+y)^2-z^2\) \((x+y-z)(x+y+z)\) |
| Sum and product of same terms \((2x - \sqrt{y})(2x + \sqrt{y})\) \((2x)^2 - (\sqrt{y})^2\) \(4x^2 - y\) |
| \((x+y-1)(x+y+1)\) \([(x+y)-1][(x+y)+1]\) \((x+y)^2-1^2\) \(x^2+2xy+y^2-1\) |
| Square of a Sum |
|---|
| \((A+B)^2=A^2+2AB+B^2\) |
| \((3x+5)^2\) \((3x)^2 + 2(3x)(5) + (5)^2\) \(9x^2+30x+25\) |
| Perfect Square \(x^2+6x+9\) \(x^2+2x3+3^2\) \((x+3)^2\) |
| Square of a Difference |
|---|
| \((A-B)^2=A^2-2AB+B^2\) |
| Perfect Square \(4x^2-4xy+y^2\) \((2x)^2-2(2x)(y)+y^2\) \((2x-y)^2\) |
| Cube of a sum |
|---|
| \((A+B)^3=A^3+3A^2B+3AB^2+B^3\) |
i.e. (see cube of a difference)
| Cube of a difference |
|---|
| \((A-B)^3=A^3-3A^2B+3AB^2-B^3\) |
| \((x^2-2)^3\) \((x^2)^3-3(x^2)^2(2)+3(x^2)(2)^2-2^3\) \(x^6-6x^4+12x^2-8\) |
| Difference of Cubes |
|---|
| \(A^3-B^3=(A-B)(A^2+AB+B^2)\) |
| \(27x^3-1\) \((3x)^3-1^3\) \((3x-1)((3x)^2+(3x)(1)+1^2)\) \((3x-1)(9x^2+3x+1)\) |
| Sum of Cubes |
|---|
| \(A^3+B^3=(A+B)(A^2-AB+B^2)\) |
| \(x^6+8\) \((x^2)^3+2^3\) \((x^2+2)((x^2)^2-(x^2)2+2^2)\) \((x^2+2)(x^4-2x^2+4)\) |
Rational Expressions
A rational expression is a fractional expression in which both the numerator and the denominator are polynomials. A rational expression is the quotient of two polynomials. A compound fraction is a fraction in which the numerator, the denominator, or both, are themselves fractional expressions.
Simplifying Rational Expressions
Steps might include: reduce, factor, cancel, & distribute.
| Simplify | \(x^2-1 \over x^2+x-2\) |
|---|---|
| Factor | \((x-1)(x+1) \over (x-1)(x+2)\) |
| Cancel | \(x+1 \over x+2\) |
| Simplify | \(3(x+2)(x+1) \over 6(x-1)^2\) |
|---|---|
| Reduce | \((x+2)(x+1) \over 2(x-1)^2\) |
| Cancel | \(x+2 \over 2(x-1)\) |
| Distribute | \(x+2 \over 2x-2\) |
| Simplify | \(y^2-3y-18 \over 2y^2+5y+3\) |
|---|---|
| Factor Quadratic Trinomials | \((y^2+3y)+(-6y-18) \over (2y^2+2y)+(3y+3)\) |
| Factor y from \((y^2+3y)\) and -6 from \((-6y-18)\) |
\(y(y+3)-6(y+3)\) |
| Factor 2y from \((2y^2+2y)\) and 3 from \((3y+3)\) |
\(2y(y+1)+3(y+1)\) |
| Factor out GCF | \((y+3)(y-6) \over (y+1)(2y+3)\) |
Multiplying and Dividing Rational Expressions
The same rules that govern the multiplication & division of fractions, are directly applicable to the multiplication & division of rational expressions.
| Multiplication | \({x^2+2x-3 \over x^2+8x+16} \cdot {3x+12 \over x-1}\) |
|---|---|
| Factor Numerators | \((x-1)(x+3) \cdot 3(x+4)\) |
| Factor Denominators | \((x+4)(x+4) \cdot (x+1)\) |
| \(3(x-1)(x+3)(x+4) \over (x-1)(x+4)^2\) | |
| Cancel | \(3(x+3) \over x+4\) |
| Division | \({x-4 \over x^2-4} \div {x^2-3x-4 \over x^2+5x+6}\) |
|---|---|
| Apply | \({x-4 \over x^2-4} \cdot {x^2+5x+6 \over x^2-3x-4}\) |
| Factor Numerators | \(x-4 \cdot {x^2+5x+6}\) |
| \((x-4) \cdot (x+2)(x+3)\) | |
| Factor Denominators | \({x^2-4} \cdot {x^2-3x-4}\) |
| \(x^2-2^2=(x-2)(x+2)\) | |
| \((x-2)(x+2) \cdot (x+1)(x-4)\) | |
| Cancel | \(x+3 \over (x+1)(x-2)\) |
| \(x+3 \over x^2-x-2\) |
Adding and Subtracting Rational Expressions
The same rules that govern the addition & subtraction of fractions, are directly applicable to the addition & subtraction of rational expressions.
| Addition | \(\frac{3}{x-1} + \frac{x}{x+2}\) |
|---|---|
| Find the LCD | \((x-1)(x+2)\) |
| \((\frac{3}{x-1} \cdot \frac{x+2}{x+2}) + (\frac{x}{x+2} \cdot \frac{x-1}{x-1})\) | |
| \(\frac{3(x+2)}{(x-1)(x+2)} + \frac{x(x-1)}{(x+2)(x-1)}\) | |
| \(\frac{3x+6+x^2-x}{(x-1)(x+2)}\) | |
| Combine like terms | \(\frac{x^2+2x+6}{(x-1)(x+2)}\) |
| \(\frac{x^2+2x+6}{x^2+x-2}\) |
| Addition & Subtraction | \(\frac{3}{x}+\frac{x-1}{x+2}-\frac{x}{x-5}\) |
|---|---|
| Find the LCD | \((\frac{3}{x} \cdot \frac{(x+2)(x-5)}{(x+2)(x-5)}) + (\frac{x-1}{x+2} \cdot \frac{x(x-5)}{x(x-5)}) - (\frac{x}{x-5} \cdot \frac{x(x+2)}{x(x+2)})\) |
| \(\frac{3(x^2-3x-10)}{x(x+2)(x-5)} + \frac{x-1(x^2-5x)}{x(x+2)(x-5)} - \frac{x(x^2+2x)}{x(x+2)(x-5)}\) | |
| Distribute | \(\frac{3x^2-9x-30+x^3-6x^2+5x-x^3-2x^2}{x(x+2)(x-5)}\) |
| Group like terms | \(\frac{(x^3-x^3)+(3x^2-6x^2-2x^2)+(-9x+5x)-30}{x(x+2)(x-5)}\) |
| Combine like terms | \(\frac{-5x^2-4x-30}{x(x+2)(x-5)}\) |
| \(\frac{-5x^2-4x-30}{x^3-3x^2-10x}\) |
Simplifying Compound Fractions
| Simplify (Method A) | \(\frac x y + 1 \over 1 - \frac y x\) |
|---|---|
| Convert expression into a fraction |
\(\frac x y + \frac 1 1 \over \frac 1 1 - \frac y x\) |
| Expand to get LCD | \(\frac x y + (\frac 1 1 \cdot \frac y y) \over (\frac 1 1 \cdot \frac x x) - \frac y x\) |
| \(\frac{x+y}{y} \div \frac{x-y}{x}\) | |
| Take the reciprocal of the second fraction and flip the sign |
\(\frac{x+y}{y} \cdot \frac{x}{x-y}\) |
| \(\frac{x(x+y)}{y(x-y)}\) |
| Simplify (Method B) | \(\frac x y + 1 \over 1 - \frac y x\) |
|---|---|
| Find LCD of ALL fractions (xy) |
\(\frac{\frac{x}{y} + 1}{1 - \frac{y}{x}} \cdot \frac{xy}{xy}\) |
| \(\frac{xy(\frac{x}{y} + 1)}{xy(1 - \frac{y}{x})}\) | |
| \(\frac{x^2+xy}{xy-y^2}\) | |
| Factor | \(\frac{x(x+y)}{y(x-y)}\) |
| Simplify | \(\frac{\frac{1}{a+h}-\frac{1}{a}}{h}\) |
|---|---|
| Find the LCD \(a(a+h)\) | \(\frac{(\frac{1}{a+h} \cdot \frac{a}{a}) - (\frac{1}{a} \cdot \frac{a+h}{a+h})}{h}\) |
| \(\frac{\frac{a}{a(a+h)} - \frac{a+h}{a(a+h)}}{h}\) | |
| \(\frac{a-(a+h)}{a(a+h)} \over h\) | |
| \(\frac{a-(a+h)}{a(a+h)} \cdot \frac{1}{h}\) | |
| \(\frac{-h}{a(a+h)} \cdot \frac{1}{h}\) | |
| Cancel common factors | \(\frac{-1}{a(a+h)}\) |
| Simplify |
|---|
| \(\frac{\frac{x+2}{x-1}-\frac{x-3}{x-2}}{x+2}\) |
| \(\frac{\frac{(x-2)(x+2)-(x-1)(x-3)}{(x-1)(x-2)}}{x+2}\) |
| \(\frac{\frac{(x^2-4)-(x^2-3x-x+3)}{(x-1)(x-2)}}{x+2}\) |
| \(\frac{\frac{x^2-4-x^2+3x+x-3}{(x-1)(x-2)}}{x+2}\) |
| \(\frac{\frac{(x^2-x^2)+(3x+x)+(-4-3)}{(x-1)(x-2)}}{x+2}\) |
| \(\frac{\frac{4x-7}{(x-1)(x-2)}}{x+2}\) |
| \(\frac{4x-7}{(x-1)(x-2)} \div x+2\) |
| \(\frac{4x-7}{(x-1)(x-2)} \cdot \frac{1}{x+2}\) |
| \(\frac{4x-7}{(x-1)(x-2)(x+2)}\) |
| \(\frac{4x-7}{(x-1)(x^2-4)}\) |
| \(\frac{4x-7}{x^3-x^2-4x+4}\) |
Simplifying Compound Fractions With Fractional Exponents
Problems of this nature are found in calculus.
| Factor out the power of \(1+x^2\) with the smallest exponent, in this case \((1+x^2)^{-\frac{1}{2}}\) |
\(\frac{(1+x^2)^\frac{1}{2} - x^2(1+x^2)^{-\frac{1}{2}}}{1+x^2}\) |
|---|---|
| To factor out \((1+x^2)^{-\frac{1}{2}}\) from \((1+x^2)^{\frac{1}{2}}\), we subtract exponents: i.e. \((1+x^2)^{\frac{1}{2}-(-\frac{1}{2})}\) \((1+x^2)^{\frac{1}{2}+\frac{1}{2}=\frac{2}{2}=1}\) \((1+x^2)\) |
\(\frac{(1+x^2)^{-\frac{1}{2}}\left[(1+x^2)-x^2\right]}{1+x^2}\) |
| Distribute | \(\frac{(1+x^2)^{-\frac{1}{2}}\left[1+x^2-x^2\right]}{1+x^2}\) \(\frac{(1+x^2)^{-\frac{1}{2}}}{(1+x^2)^1}\) |
| Divide expression by subtracting exponents. Remember, \(\frac{dividend}{divisor}=dividend \div divisor.\) Therefore: \(-\frac{1}{2}-1=-\frac{3}{2}\) |
\((1+x^2)^{-\frac{3}{2}}\) |
| Implement negative power rule by taking the reciprocal |
\(\frac{1}{(1+x^2)^{\frac{3}{2}}}\) |
Equations & Inequalities
Solving Linear Equations
The linear equation in one variable is an equation equivalent to one of the form: \(ax+b=0\), where a and b are real numbers and x is the variable.
| Properties of Equations |
|---|
| \(A=B <=> A+C=B+C\) |
| \(A=B <=> CA=CB, \, where \, C \ne 0\) |
| Solving | \(7x-4=3x+8\) |
|---|---|
| Simplify (Distribute & Combine like terms) |
\(\) |
| Transpose | \(7x=3x+8+4\) |
| \(7x-3x=8+4\) | |
| Simplify (Distribute & Combine like terms) |
\(4x=12\) |
| Divide by Coefficient (or multiply by reciprocal of coefficient) |
\(\frac{4x}{4}=\frac{12}{4}\) |
| \(x=3\) |
Solving For One Variable In Terms of Others
| Isolate M by factoring | \(F=G\frac{mM}{r^2}\) |
|---|---|
| Factor | \(F=(\frac{Gm}{r^2})M\) |
| Multiply by the reciprocal of \(\frac{Gm}{r^2}\) to cancel |
\((\frac{r^2}{Gm})F=(\frac{r^2}{Gm})(\frac{Gm}{r^2})M\) |
| \(M = \frac{r^2F}{Gm}\) |
| Isolate w by factoring | \(A=2lw+2wh+2lh\) |
|---|---|
| Factor/Isolate w by first collecting terms with w |
\(A=(2lw+2wh)+2lh\) |
| \(A=w(2l+2h)+2lh\) | |
| Transpose 2lh | \(A-2lh=w(2l+2h)\) |
| Divide by coefficient to clear rhs |
\(\frac{A-2lh}{(2l+2h)}=\frac{w(2l+2h)}{(2l+2h)}\) |
| Transpose 2lh | \(w=\frac{A-2lh}{2l+2h}\) |
Solving Quadratic Equations
Quadratic equations are equations of the form: \(ax^2+bx+c=0\), where a, b, and c are real numbers with \(a \ne 0\). Understand also, the Zero-Product Property, which states, that \(AB=0\) if and only if A = 0 or B = 0.
| Solve by Factoring | \(x^2+5x=24\) |
|---|---|
| Transpose | \(x^2+5x-24=0\) |
| Factor Trinomial | \(x^2-3x+8x-24=0\) |
| \(x(x-3)+8(x-3)=0\) | |
| \((x-3)(x+8)=0\) | |
| Solutions | \(x-3=0, x=3\) \(x+8=0, x=-8\) |
| Solve by Completing the Square | \(x^2-8x+13=0\) |
|---|---|
| Transpose | \(x^2-8x=-13\) |
| Complete the Square | \(x^2-8x+(\frac{-8}{2})^2=-13+(\frac{-8}{2})^2\) |
| \(x^2-8x+16=-13+16\) | |
| \(x^2-8x+16=3\) | |
| Factor | \((x-4)(x-4)=3\) |
| \((x-4)^2=3\) | |
| Take the Square | \(x-4=\sqrt{3}\) |
| Transpose | \(x=4 \pm \sqrt{3}\) |
| Completeing the Square where leading coefficient \(a \ne 1\) |
\(3x^2-12x+6=0\) |
|---|---|
| Transpose | \(3x^2-12x=-6\) |
| You must factor the leading coefficient from both terms that contain x, before completing the square |
\(3(x^2-4x)=3(-2)\) |
| \(3(x^2-4x+(\frac{-4}{2})^2)=3(-2+(\frac{-4}{2})^2)\) | |
| \(3(x^2-4x+4)=3(-2+4)\) | |
| \(3((x-2)(x-2))=6\) | |
| \(3(x-2)^2=6\) | |
| \(\frac{3(x-2)^2}{3}=\frac{6}{3}\) | |
| \((x-2)^2=2\) | |
| \(\sqrt{(x-2)^2}=\sqrt 2\) | |
| \(x-2=\sqrt 2\) | |
| \(x=2 \pm \sqrt 2\) |
| Solve by Quadratic Equation | \(ax^2+bx+c=0\) |
|---|---|
| Formula | \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\) |
| Problem | \(3x^2-5x-1=0\) |
| Variables | a=3, b=-5, c=-1 |
| Solve | \(x = {-(-5) \pm \sqrt{(-5)^2-4(3)(-1)} \over 2(3)}\) |
| \(x = {5 \pm \sqrt{25+12} \over 6}\) | |
| Solution | \(x = {5 \pm \sqrt{37} \over 6}\) |
| Solve by Quadratic Equation | \(ax^2+bx+c=0\) |
|---|---|
| Formula | \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\) |
| Problem | \(x^2+2x+2=0\) |
| Variables | a=1, b=2, c=2 |
| Solve | \(x = {-(2) \pm \sqrt{(2)^2-4(1)(2)} \over 2(1)}\) |
| \(x = {-2 \pm \sqrt{4-8} \over 2}\) | |
| \(x = {-2 \pm \sqrt{-4} \over 2}\) | |
| \(x = {-2 \pm \sqrt{-1} \cdot \sqrt{4} \over 2}\) | |
| \(x = {-2 \pm 2i \over 2}\) | |
| \(x = {-1 \pm 1i}\) |
Solving Linear Inequalities
Pay special attention to rules 3 & 4. Remember, that what is true for multiplication, is also true for division in this instance.
| Inequalities, Rules For | |
|---|---|
| Adding the same quantity to each side of an inequality gives an equivalent inequality |
\(A \le B <=> A + C \le B + C\) |
| Subtracting the same quantity from each side of an inequality gives an equivalent inequality |
\(A \le B <=> A - B \le B - C\) |
| Multiplying each side of an inequality by the same positive quantity gives an equivalent inequality |
\(A \le B <=> CA \le CB\) \(If \, C > 0\) |
| Multiplying each side of an inequality by the same negative quantity reverses the direction of the inequality |
\(A \le B <=> CA \ge CB\) \(If \, C > 0\) |
| Taking Reciprocals of each side of an inequality involving positive quantities reverses the direction of the inequality |
\(A \le B <=> \frac{1}{A} \ge \frac{1}{B}\) \(If \, A > 0 \, and \, B > 0\) |
| Inequalities can be added | \(A+C \le B+D\) \(If \, A \le B \, and \, C \le D\) |
An inequality is linear when/if each term is constant or a multiple of the variable. To solve, isolate the variable on one side of the inequality sign.
| Linear Inequality | \(3x \lt 9x + 4\) |
|---|---|
| \(3x - 9x \lt 4\) | |
| \(-6x \lt 4\) | |
| \(\frac{-6x}{-6} \gt \frac{4}{-6}\) | |
| Same as above | \((-\frac{1}{6})(-6x) \gt (-\frac{1}{6})(4)\) or \((-\frac{1}{6})(\frac{-6x}{1}) \gt (-\frac{1}{6})(\frac{4}{1})\) |
| Solution | \(x \gt -\frac{2}{3}\) |
| Solution Set | \((-\frac{2}{3}, \infty)\) |
The solution set consists of all numbers greater than \(-\frac{2}{3}\), In other words, the solution of the inequality is the interval \((-\frac{2}{3}, \infty)\).
Solving a Pair of Simultaneous Inequalities
| Simultaneous | \(4 \le 3x - 2 \lt 13\) |
|---|---|
| Transpose | \(4 + (2) \le 3x - 2 + (2) \lt 13 + (2)\) |
| \(6 \le 3x \lt 15\) | |
| Divide by Coefficient | \(\frac{6}{3} \le \frac{3x}{3} \lt \frac{15}{3}\) |
| \(2 \le x \lt 5\) | |
| Solution Set | \([2,5)\) |
Solving Absolute Value Equations
| \(\vert 3x+1\vert = 7\) | |
|---|---|
Solving Absolute Value Inequalities
| \(\vert x-4\vert-3<6\) | |
|---|---|
Complex Numbers
| Complex Numbers |
|---|
| \(i = \sqrt{-1}\) |
| \(i^2 = -1\) \(\sqrt[n]{x} \cdot \sqrt[n]{x} = x\) |
| \(i^3 = -i\) \(-\sqrt{-1}\) |
| \(i^4 = 1\) \(-1\cdot\sqrt{-1}\cdot\sqrt{-1}\) \(i\cdot i\cdot i\cdot i\) \((i\cdot i)\cdot (i\cdot i)\) \(-1\cdot-1=1\) |
| \(i^5 = i\) |
Logarithms
| Properties of Logarithms | |
|---|---|
| \(\log_b y=x, \, y=b^x\) | |
| Product | \(\log_b xy = \log_b x + \log_b y\) |
| Quotient | \(\log_b \frac{x}{y} = \log_b x - \log_b y\) |
| Power | \(\log_b x^p = p \cdot \log_b x\) |
| Change of Base | \(\log_a x = \frac{\log_b x}{\log_b a}\) |
| Equality | \(\log_b x = \log_b y, \, x=y\) |
Functions
Applications
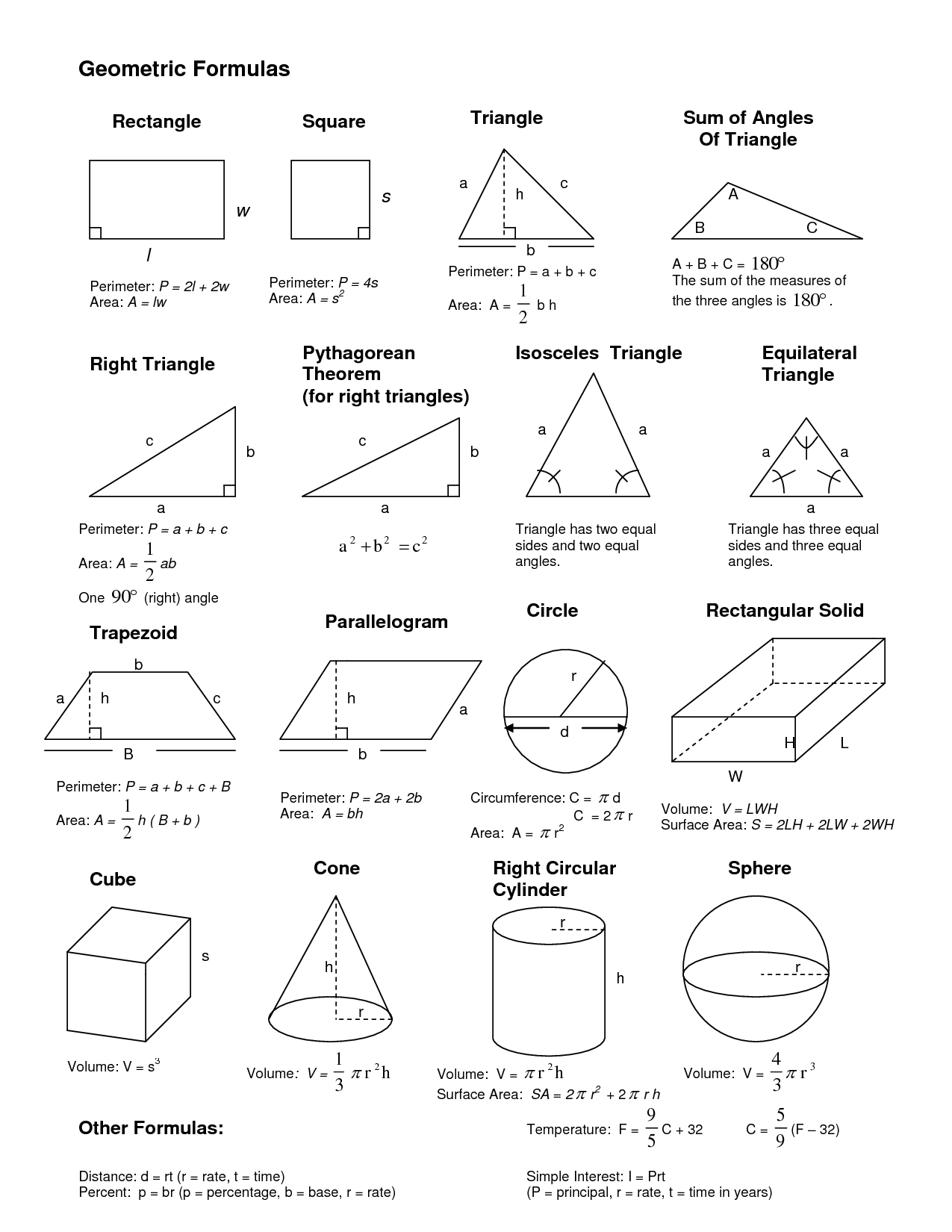
Pythagorean Theorem
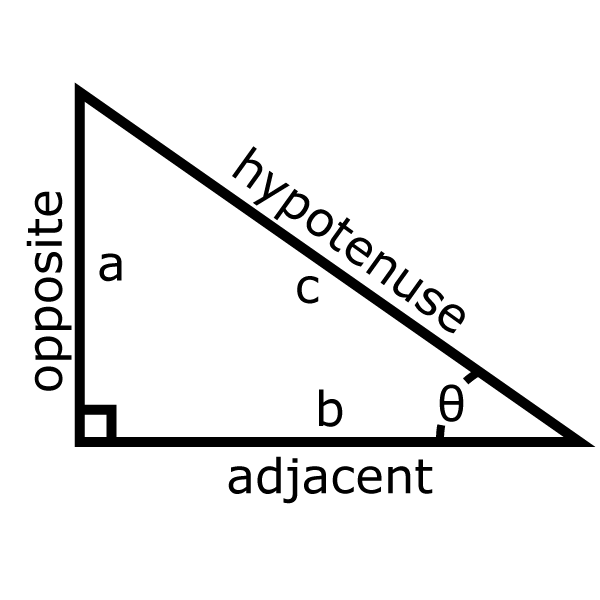
We can use the Pythagorean Theorem to calculate the length of a diagonal. Remember that \(a^2 + b^2 = c^2\) or alternatively \(c = \sqrt{a^2 + b^2}\), where c represents the diagonal or hypotenuse. The Pythagorean Theorem utilizes the opposite & adjacent legs of the right triangle to find the hypotenuse.
| Pythagorean Theorem | \(a=7 ft, \, b=8 ft\) |
|---|---|
| Substitute | \(a^2 + b^2 = c^2\) \((7 \, ft)^2 + (8 \, ft)^2 = c^2\) |
| Square | \(49 \, ft^2 + 64 \, ft^2 = c^2\) |
| Combine | \(113 \, ft^2 = c^2\) |
| Square Both Sides | \(\sqrt{113 \, ft^2} = \sqrt{c^2}\) |
| Solution | \(c = 10.63014581273465 \, ft\) |
| Round to tenths place | \(c = 10.63 \, ft\) |
Common Formulas
There are a few common formulas you should be familiar with below before moving on to the next article.